Python配对交易策略统计套利量化交易分析股票市场|附代码数据
说到在股票市场上赚钱,有无数种不同的赚钱方式。似乎在金融界,无论你走到哪里,人们都在告诉你应该学习 Python
毕竟,Python 是一种流行的编程语言,可用于所有类型的领域,包括数据科学。有大量软件包可以帮助您实现目标,许多公司使用 Python 来开发与金融界相关的以数据为中心的应用程序和科学计算。
最重要的是,Python 可以帮助我们利用许多不同的交易策略,这些策略(没有它)将很难用手或电子表格进行分析。我们将讨论的交易策略之一称为 配对交易。
配对交易
配对交易是_均值回归的_一种形式 ,具有始终对冲市场波动的独特优势。该策略基于数学分析。
原理如下。假设您有一对具有某种潜在经济联系的证券 X 和 Y。一个例子可能是生产相同产品的两家公司,或一条供应链中的两家公司。如果我们可以用数学模型对这种经济联系进行建模,我们就可以对其进行交易。
为了理解配对交易,我们需要理解三个数学概念: 平稳性、差分和协整。
import numpy as np
import pandas as pd
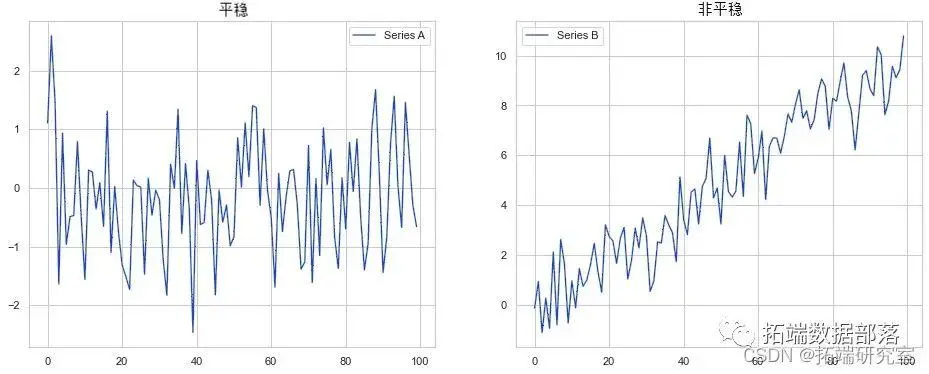
平稳/非平稳
平稳性是时间序列分析中最常见的未经检验的假设。当数据生成过程的参数不随时间变化时,我们通常假设数据是平稳的。或者考虑两个系列:A 和 B。系列 A 将生成具有固定参数的平稳时间序列,而 B 将随时间变化。
我们将创建一个函数,为概率密度函数创建 z 分数。高斯分布的概率密度为:
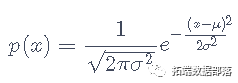
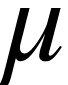 是均值和
是均值和 是标准差。标准差的平方,
是标准差。标准差的平方, ,是方差。经验法则规定 66% 的数据应该介于
,是方差。经验法则规定 66% 的数据应该介于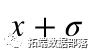 和
和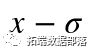 ,这意味着该函数
,这意味着该函数normal 更有可能返回靠近均值的样本,而不是那些远离均值的样本。musigmareturn normal(mu, sigma )从那里,我们可以创建两个展示平稳和非平稳时间序列的图。
# 设置参数和数据点数
T = 100
Series(index=range(T))
# 现在参数依赖于时间
# 具体来说,序列的均值随时间变化
B[t] = genedata
plt.subplots
为什么平稳性很重要
许多统计测试要求被测试的数据是平稳的。在非平稳数据集上使用某些统计数据可能会导致垃圾结果。作为一个例子,让我们通过我们的非平稳
np.mean
plt.figure
plt.plot
plt.hlines
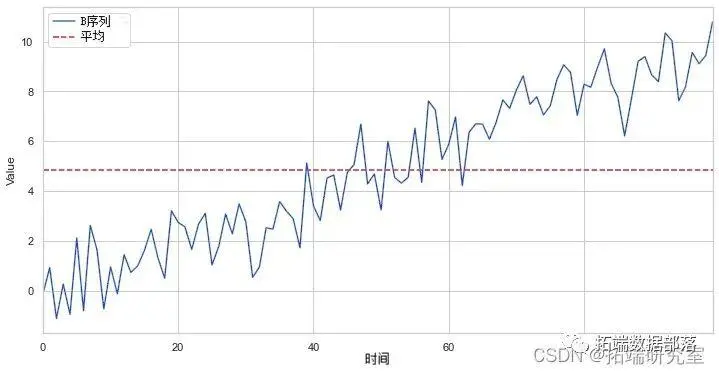
计算的平均值将显示所有数据点的平均值,但对未来状态的任何预测都没有用。与任何特定时间相比,它毫无意义,因为它是不同时间的不同状态混搭在一起的集合。这只是一个简单而清晰的例子,说明了为什么非平稳性会扭曲分析,在实践中会出现更微妙的问题。
平稳性检验Augmented Dickey Fuller(ADF)
为了测试平稳性,我们需要测试一个叫做_单位根的_东西 。自回归单位根检验基于以下假设检验:
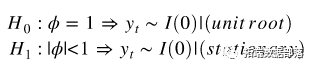
它被称为单位根 tet 因为在原假设下,自回归多项式![]() , 的根等于 1。
, 的根等于 1。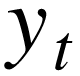
在原假设下趋势平稳。如果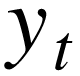 然后首先进行差分,它变成:
然后首先进行差分,它变成: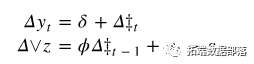
检验统计量为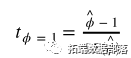
![]() 是最小二乘估计和 SE(
是最小二乘估计和 SE(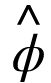 ) 是通常的标准误差估计。该测试是单侧左尾测试。如果 {
) 是通常的标准误差估计。该测试是单侧左尾测试。如果 {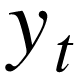 } 是平稳的,那么可以证明
} 是平稳的,那么可以证明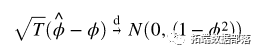 或者
或者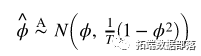 并且是
并且是![]() ,然而,在非平稳性原假设下,上述结果给出
,然而,在非平稳性原假设下,上述结果给出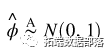 以下函数将允许我们使用 Augmented Dickey Fuller (ADF) 检验来检查平稳性。
以下函数将允许我们使用 Augmented Dickey Fuller (ADF) 检验来检查平稳性。
defty_test(X, cutoff=0.01):
# adfuller 中的 H_0 是单位根存在(非平稳)
# 我们必须观察显着的 p 值看该序列是平稳的
adfuller

正如我们所见,基于时间序列 A 的检验统计量(与特定的 p 值对应),我们可能无法拒绝原假设。因此,A 系列很可能是静止的。另一方面,B系列被假设检验拒绝,所以这个时间序列很可能是非平稳的。
协整
金融数量之间的相关性是出了名的不稳定。尽管如此,几乎所有的多元金融问题都经常使用相关性。相关性的另一种统计度量是协整。这可能是衡量两个金融数量之间联系的更稳健的衡量标准,但迄今为止,几乎没有基于此概念的偏差理论。
两只股票可能在短期内完全相关,但从长远来看却出现分歧,一只增长,另一只下跌。相反,两只股票可能相互跟随,相距不会超过一定距离,但具有相关性,正负相关变化。如果我们是短期,相关性可能很重要,但如果我们在投资组合中长期持有股票,则无关紧要。
我们已经构建了两个协整序列的示例。我们现在绘制两者之间的差异。
# 生成每日收益
np.random.normal
# 总结
plot
np.random.normal
Y = X + 6 + 噪音
plt.show()
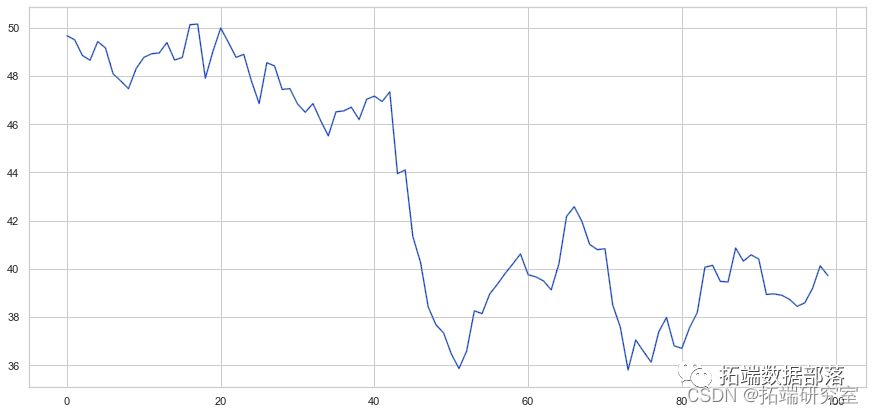
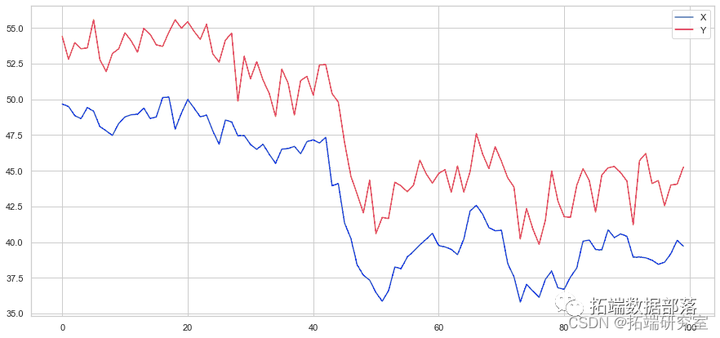
(Y - X).plot # 绘制点差
plt.axhline# 添加均值
plt.xlabel
plt.xlim

This message is used to verify that this feed (feedId:71868927651309568) belongs to me (userId:71868763667313664). Join me in enjoying the next generation information browser https://follow.is.
Good article! We will be linking to his particularly great poat
on our site. Keeep up the good writing. https://Fortune-glassi.mystrikingly.com/
I don’t think the title of your article matches the content lol. Just kidding, mainly because I had some doubts after reading the article.