贝叶斯定理是由英国数学家托马斯・贝叶斯（Thomas Bayes）提出的。托马斯・贝叶斯生活在 18 世纪，他生前并未发表关于这个定理的内容。在他去世后，他的朋友理查德・普莱斯（Richard Price）在整理他的遗稿时发现了关于贝叶斯定理的研究，并将其发表在 1763 年的《皇家学会哲学学报》上。
贝叶斯定理的提出是为了解决在不确定情况下进行推理和决策的问题。它提供了一种基于先验知识和新证据来更新对事件概率估计的方法。

01

贝叶斯定理的定义

贝叶斯定理描述了在已知某些事件发生的条件下，另一个事件发生的概率。其公式表示为：

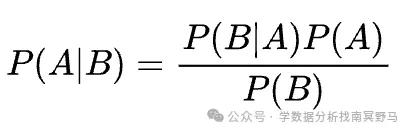
其中，P(A|B)表示在事件B发生的条件下事件A发生的概率，称为后验概率；P(B|A)表示在事件A发生的条件下事件B发生的概率；P(A)是事件A的先验概率，即在没有任何新证据的情况下事件A发生的概率；P(B)为事件B发生的概率
贝叶斯定理的核心思想是：后验概率 = 先验概率× 似然度 ÷ 标准化常量。简单来说，贝叶斯定理就是通过先验概率和新的证据（似然度）来计算后验概率，从而不断更新我们对事件的认识。先验概率是我们在没有任何新证据的情况下对事件的初始判断，似然度则是新证据出现的可能性，标准化常量用于确保后验概率的总和为 1。通过不断地收集新证据并更新先验概率，我们可以逐渐逼近事件的真实概率。02

贝叶斯定理的案例解析

案例一：疾病监测

假设有一种罕见疾病，在人群中的发病率为0.1%（即先验概率P(患病)=0.001），现在有一种检测方法，对于患病的人，检测结果为阳性的概率为99%（即P(阳性|患病)=0.99），对于未患病的人，检测结果为阳性的概率为1%（即P(阳性|未患病)=0.01）

现在有一个人检测结果为阳性，求这个人真正患病的概率（即后验概率P(患病|阳性)）

案例二：邮件分类

假设在一个邮箱中，垃圾邮件的比例为20%（即先验概率P(垃圾邮件)=0.2），已知在垃圾邮件中出现特定关键词“优惠”的概率为80%（即P(优惠|垃圾邮件)=0.8），在正常邮件中出现“优惠”的概率为5%（即P(优惠|正常邮件)=0.05）

现在收到一封邮件含有“优惠”这个关键词，求这封邮件为垃圾邮件的概率（即后验概率P(垃圾邮件|优惠)）

03

贝叶斯定理在AB实验中的应用

案例一：网站转化率测试

背景：某电商平台有两个不同的首页设计方案A和B，需要通过AB测试确定哪个方案能带来更高的用户转化率。
数据过程测算演示：
设定先验概率：假设先验认为两个方案的转化率相同，即先验转化率P(A) = P(B) = 0.5%
收集实验数据：随机分配用户到A和B两个方案，各获得10000次访问量。A方案转化了55次，B方案转化了60次
应用贝叶斯定理：
1、计算似然比：
P(数据|A) = C(10000, 55) * 0.005^55 * 0.995^9945
P(数据|B) = C(10000, 60) * 0.005^60 * 0.995^9940
2、更新后验概率：
P(A|数据) = P(数据|A) * P(A) / (P(数据|A) * P(A) + P(数据|B) * P(B))
P(B|数据) = P(数据|B) * P(B) / (P(数据|A) * P(A) + P(数据|B) * P(B))
3、结果解释：
计算得出P(B|数据) > P(A|数据)，说明在给定数据下，B方案有更高的后验概率带来更高的转化率

案例二：搜索引擎广告效果测试

背景：某搜索引擎测试两种不同的广告展示策略A和B，以观察哪种策略能带来更高的点击率
数据过程测算演示：
设定先验概率：基于历史数据，假设A策略的先验点击率为0.5%，B策略的先验点击率也为0.5%
收集实验数据：各向100,000名用户展示A和B策略的广告，A策略获得480次点击，B策略获得520次点击
应用贝叶斯定理：
1、计算似然比：与案例一类似，使用二项分布计算P(数据|A)和P(数据|B)。
2、更新后验概率：同样使用贝叶斯公式更新A和B策略的后验点击率概率。
3、结果解释：计算结果显示P(B|数据)高于P(A|数据)，说明在给定数据下，B策略有更高的后验概率带来更高的点击率。04

贝叶斯定理的python代码实现

基于以上AB实验的两个案例，采用Python代码实现出来

import math
from scipy.special import comb

def bayesian_update(prior_a, prior_b, data_a, data_b, total_a, total_b):
    # 计算似然比
    likelihood_a = comb(total_a, data_a) * (prior_a ** data_a) * ((1 - prior_a) ** (total_a - data_a))
    likelihood_b = comb(total_b, data_b) * (prior_b ** data_b) * ((1 - prior_b) ** (total_b - data_b))
    
    # 更新后验概率
    posterior_a = likelihood_a * prior_a / (likelihood_a * prior_a + likelihood_b * prior_b)
    posterior_b = likelihood_b * prior_b / (likelihood_a * prior_a + likelihood_b * prior_b)
    
    return posterior_a, posterior_b

# 案例一：网站转化率测试
prior_conversion_a = 0.005
prior_conversion_b = 0.005
total_visits_a = 10000
total_visits_b = 10000
conversions_a = 55
conversions_b = 60

posterior_conversion_a, posterior_conversion_b = bayesian_update(
    prior_conversion_a, prior_conversion_b, conversions_a, conversions_b, total_visits_a, total_visits_b
)

print(f"案例一后验转化率：A方案 {posterior_conversion_a:.4f}，B方案 {posterior_conversion_b:.4f}")

# 案例二：搜索引擎广告效果测试
prior_click_a = 0.005
prior_click_b = 0.005
total_users_a = 100000
total_users_b = 100000
clicks_a = 480
clicks_b = 520

posterior_click_a, posterior_click_b = bayesian_update(
    prior_click_a, prior_click_b, clicks_a, clicks_b, total_users_a, total_users_b
)

print(f"案例二后验点击率：A策略 {posterior_click_a:.4f}，B策略 {posterior_click_b:.4f}")

这段代码定义了一个bayesian_update函数，用于计算并更新后验概率。然后，它分别使用两个案例的数据来调用这个函数，并打印出后验转化率或后验点击率。

最后，再拓展一下，贝叶斯和显著性检验（例如Z检验和T检验）在AB实验应用时的区别：

1、核心思想不同

*贝叶斯定理关注于在获取新数据后，如何更新对某一假设的信念程度，即后验概率。它允许实验者结合先验知识和实验数据，进行更灵活的决策

*显著性检验则是一种统计推断方法，用于判断样本与总体或两个样本之间是否存在显著差异。它主要关注实验结果是否具有统计学意义上的显著性。

2、应用方式不同

*贝叶斯定理在AB实验中，可以用于实时更新两个版本（A和B）的效果概率，根据后验概率的变化，实验者可以灵活调整实验策略或提前结束实验。

*显著性检验通常在实验结束后进行，通过计算统计量（如Z值、t值等）并与临界值比较，来判断实验结果是否显著。

3、结果解释不同

*贝叶斯定理的结果是一个概率值，表示在给定数据下，某一假设为真的信念程度。它提供了关于假设更直观、更易于理解的信息。

*显著性检验的结果通常是一个P值，表示在原假设为真的条件下，观测到当前数据或更极端数据的概率。P值小于显著性水平（如0.05）时，通常认为实验结果显著，但P值本身并不直接反映效应大小或实验结果的实用性。

总而言之，在AB实验中，两者可以结合使用，贝叶斯定理用于实验过程中的实时决策支持，显著性检验用于实验结束后的结果验证。